难度中等143
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
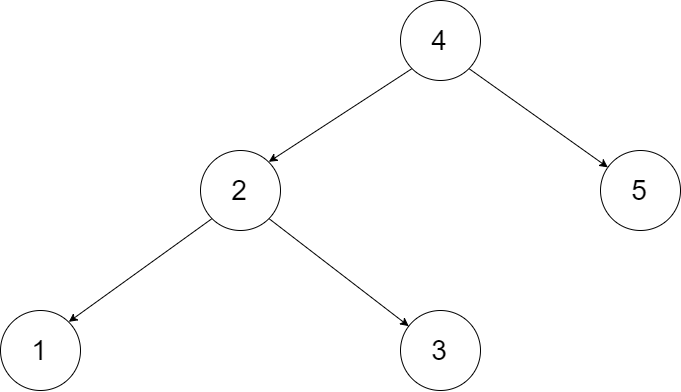
为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
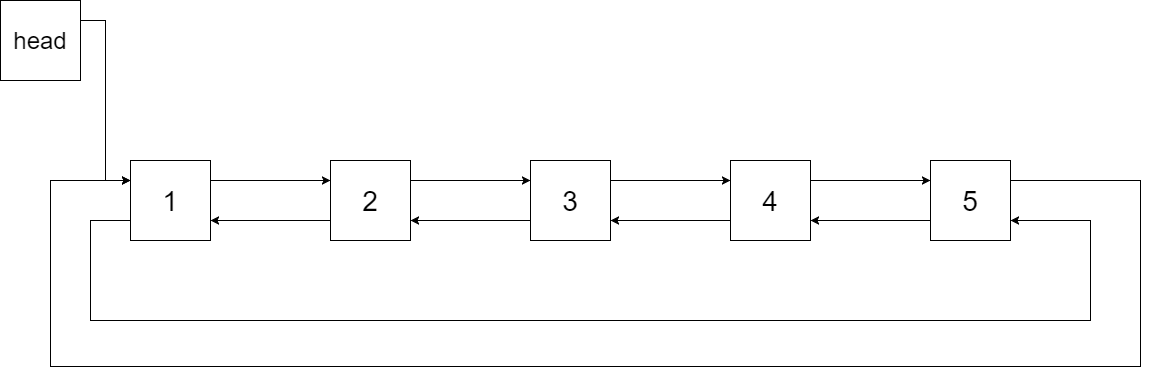
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
知道是中序遍历,但是没有想出递归的解法, 想通过迭代完成,迭代没有写出来,参考了题解之后写出了递归。关键是要构建头和尾指针,中序遍历一开始一直想左走,直到空,并且这时更新head的值,返回时用tail记录前一个节点,更新前一个节点和当前节点的指针关系。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 class Solution {public : Node* treeToDoublyList (Node* root) { if (root == nullptr ) return nullptr ; head = nullptr ; tail = nullptr ; inorder(root); head->left = tail; tail->right = head; return head; } void inorder (Node* root) if (root == nullptr ){ return ; } else { inorder(root->left); if (tail == nullptr ) { head = root; } else { tail->right = root; root->left = tail; } tail = root; inorder(root->right); } } private : Node *head, *tail; };
难度困难94
请实现两个函数,分别用来序列化和反序列化二叉树。
示例:
1 2 3 4 5 6 7 8 9 你可以将以下二叉树: 1 / \ 2 3 / \ 4 5 序列化为 "[1,2,3,null,null,4,5]"
注意:本题与主站 297 题相同:https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree/
主要是通过层次遍历去解决。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 class Codec {public : string serialize (TreeNode* root) if (root == nullptr ) return "" ; string res = "[" ; queue <TreeNode*> q; q.push(root); res += (to_string(root->val) + ',' ); while (!q.empty()) { TreeNode* temp = q.front(); q.pop(); if (temp->left){ q.push(temp->left); res += to_string(temp->left->val); } else { res += "null" ; } res += "," ; if (temp->right){ q.push(temp->right); res += to_string(temp->right->val); } else { res += "null" ; } if (!q.empty()) res += "," ; } res += "]" ; return res; } TreeNode* deserialize (string data) { if (data.size() == 0 ) return nullptr ; string target = data.substr(1 , data.size() - 2 ); vector <TreeNode*> vec; string tmp = "" ; for (int i = 0 ; i < target.size(); ++i) { if (target[i] >= '0' && target[i] <= '9' || target[i] == '-' ) { tmp.push_back(target[i]); } else if (target[i] == ',' ) { vec.push_back(new TreeNode(atoi(tmp.c_str()))); tmp.clear(); } else { i += 4 ; vec.push_back(nullptr ); } } int pos = 1 ; for (int i = 0 ; pos < vec.size(); ++i){ if (!vec[i]){ continue ; } vec[i] -> left = vec[pos++]; if (pos < vec.size()){ vec[i] -> right = vec[pos++]; } } return vec[0 ]; } };
难度中等149
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例:
1 2 输入:s = "abc" 输出:["abc","acb","bac","bca","cab","cba"]
限制:
全排列问题有一个总结,很好,可以看一看 全排列
(回溯问题)代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution {public : vector <string > res; vector <bool > visit; vector <string > permutation(string s) { int n = s.size(); string path = "" ; visit.resize(n); for (int i = 0 ; i < n; ++i) { visit[i] = false ; } sort(s.begin(), s.end()); backTrace(s, 0 , n, path); return res; } void backTrace (const string & s,int start, int n, string path) { if (path.size() == n) { res.push_back(path); return ; } else { for (int i = 0 ; i < n; ++i) { if (!visit[i]) { if (i>0 && !visit[i-1 ] && s[i] == s[i-1 ]) continue ; path.push_back(s[i]); visit[i] = true ; backTrace(s, i, n, path); visit[i] = false ; path.pop_back(); } } } } };
难度简单96
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
1 2 输入: [1, 2, 3, 2, 2, 2, 5, 4, 2] 输出: 2
限制:
摩尔投票法,简单理解就是打仗拼兵力的问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int majorityElement (vector <int >& nums) int major = 0 , count = 0 ; for (int i = 0 ; i < nums.size(); ++i) { if (count == 0 ) { major = nums[i]; count = } else { if (major == nums[i]) ++count; else if (major != nums[i]) --count; } } return major; } };
难度简单170
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
1 2 输入:arr = [3,2,1], k = 2 输出:[1,2] 或者 [2,1]
示例 2:
1 2 输入:arr = [0,1,2,1], k = 1 输出:[0]
限制:
0 <= k <= arr.length <= 100000 <= arr[i] <= 10000
首先想到的还是构建最大堆,复杂度是O(nlogk)。但是看了题解,还知道基于快排有O(n)的解法(这也是之前面试官提过的),就尝试着写一下。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Solution {private : vector <int > res; public : vector <int > getLeastNumbers(vector <int >& arr, int k) { if (arr.empty() || k == 0 ) {return {};} return quickSelection(arr, 0 , arr.size() - 1 , k - 1 ); } vector <int > quickSelection(vector <int >& arr, int left, int right, int index) { int j = partition(arr, left, right); if (j == index) { for (int i = 0 ; i < j + 1 ; ++i) {res.push_back(arr[i]);} return res; } return j < index ? quickSelection(arr, j + 1 , right, index) : quickSelection(arr, left, j - 1 , index); } int partition (vector <int >& arr, int left, int right) int value = arr[left]; int i = left, j = right + 1 ; while (true ) { while (++ i <= right && arr[i] < value); while (-- j >= left && arr[j] > value); if (i >= j) {break ;} swap(arr[i], arr[j]); } swap(arr[left], arr[j]); return j; } void swap (int & a, int & b) int temp = a; a = b; b = temp; } };